Price Elasticity with R

Scenario
We covered Price Elasticity in an accompanying post. In this post we will look at how we can use this information to analyse our own product and cross product elasticity.
The scenario is as follows:
You are the owner of a corner mom and pop shop that sells eggs and cookies. You sometimes put a poster on your storefront advertising either your fresh farm eggs, or your delicious chocolate chip cookies. You are particularly concerned with the sales off eggs – your beautiful farm chicken would be terribly sad if they knew that their eggs were not doing so well.
Over a one month period, you collect information on sales of your eggs and the different prices you set for your product.
Data Time
We are using a modified version of Data Apple‘s data set.
You can download the supermarket data set here. In it you will find:
- Sales: the total eggs sold on the given day
- Price Eggs: the price of the eggs on the day
- Ad Type: the type of poster – 0 is the egg poster, 1 is the cookie poster.
- Price Cookies: the price of cookies on the day
Lets fire up R and load up the data
# Load data and output summary stats sales.data<-read.csv('supermarket.csv') #Look at column names and their classes sapply(sales.data,class) |
The output shows each column and its type:
Sales Price.Eggs Ad.Type Price.Cookies "integer" "numeric" "integer" "numeric" |
Since Ad.Type is a categorical variable, lets go ahead and change that and output the summary statistics of our dataset.
# Change Ad Type to factor sales.data$Ad.Type<-as.factor(sales.data$Ad.Type) summary(sales.data) |
From the results we find that:
- Sales of eggs ranged between 18 and 46
- Price of eggs ranged between $3.73 and $4.77
- We showed the egg poster 15 times and the cookies poster 15 times
- Price of cookies ranged between $4 and $4.81
Sales Price.Eggs Ad.Type Price.Cookies Min. :18.0 Min. :3.73 0:15 Min. :4.00 1st Qu.:25.2 1st Qu.:4.35 1:15 1st Qu.:4.17 Median :28.5 Median :4.48 Median :4.33 Mean :30.0 Mean :4.43 Mean :4.37 3rd Qu.:33.8 3rd Qu.:4.67 3rd Qu.:4.61 Max. :46.0 Max. :4.77 Max. :4.81 |
Right now we want to see if we can predict the relationship between Sales of Eggs, and everything else.
Regression … the Granddaddy of Prediction
We now want to run a regression and then do some diagnostics on our model before getting to the good stuff.
We can run the entire regression or add each variable to see the impact on the regression model. Since we have few predictors lets choose the latter option for fun.
# Create models m1<-lm(formula=Sales~Price.Eggs,data=sales.data) m2<-update(m1,.~.+Ad.Type) m3<-update(m2,.~.+Price.Cookies) mtable(m1,m2,m3) |
The results are pasted below. We end up with a model “m3” that has statistically significant predictors. Our model is:
Sales of Eggs = 137.37 – (16.12)Price.Eggs + 4.15 (Ad.Type) – (8.71)Price.Cookies
We look at our R2 and see that the regression explains 88.6% of the variance in the data. We also have a low mean squared error (2.611) compared to the other models we generated.
We can actually get better results by transforming our independent and dependent variables (e.g. LN(Sales)) but this will suffice for demonstrating how we can use regressions to calculate price elasticity.
Calls: m1: lm(formula = Sales ~ Price.Eggs, data = sales.data) m2: lm(formula = Sales ~ Price.Eggs + Ad.Type, data = sales.data) m3: lm(formula = Sales ~ Price.Eggs + Ad.Type + Price.Cookies, data = sales.data) ------------------------------------------------ m1 m2 m3 ------------------------------------------------ (Intercept) 115.366*** 101.571*** 137.370*** Price.Eggs -19.286*** -16.643*** -16.118*** Ad.Type: 1/0 4.195** 4.147*** Price.Cookies -8.711*** ------------------------------------------------ R-squared 0.722 0.793 0.886 adj. R-squared 0.712 0.778 0.872 sigma 3.924 3.444 2.611 ... ------------------------------------------------ |
Diagnostics
We need to test for the following assumptions whenever we do regression analysis:
1. The relationship is linear
2. The errors have the same variance
3. The errors are independent of each other
4. The errors are normally distributed
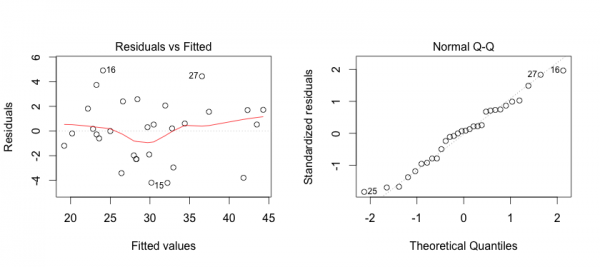
First, we can address some of these points by creating plots of the model in R.
The plot on the left shows that the residuals (errors) have no pattern in variance (Good!).
The red line is concerning because it shows some curvature indicating that perhaps the relationshp is not entirely linear (hmmm…).
On the right we see that the errors are acceptably normally distributed (they are around the straight line … Good!).
To generate this plot you can use the R code below:
# Linearity Plots par(mfrow=c(1,2)) plot(m3) # Reset grid par(mfrow=c(1,1)) |
So we want to look deeper into linearity issues. We will look at multi-colinearity first:
# Multi-collinearity library(car) vif(m3) # variance inflation factors sqrt(vif(m3)) > 2 # problem? |
The code above will show if any of the variables have multicolinearity issues that could cause issues with the model’s integrity. Generally we want values less than 2, and we have values of around 1 so we are good on this front.
Price.Eggs Ad.Type Price.Cookies 1.195107 1.189436 1.006566 |
We can generate a CERES plot to assess non-linearity:
# Diagnosis: Nonlinearity crPlots(m3) |
We see that there is definitely some issues with linearity but not to an extent that it is a cause for concern for the purpose of demonstration. So we keep calm, and move on.
Lastly we want to test independence of the residuals using the Durban Watson Test:
# Diagnosis: Non-independence of Errors durbinWatsonTest(m3) |
The output shows that there is no autocorrelation issues in the model:
lag Autocorrelation D-W Statistic p-value 1 0.06348248 1.792429 0.458 Alternative hypothesis: rho != 0 |
So we are clear to move forward with Price Elasticity and Cross Product Price Elasticity!
Price Elasticity
We now have our model:
Sales of Eggs = 137.37 – (16.12)Price.Eggs + 4.15 (Ad.Type) – (8.71)Price.Cookies
Own Price Elasticity
To calculate Price Elasticity of Demand we use the formula:
PE = (ΔQ/ΔP) * (P/Q)
(ΔQ/ΔP) is determined by the coefficient -16.12 in our regression formula.
To determine (P/Q) we will use the mean Price (4.43) and mean Sales (30).
Therefore we have PE = -16.12 * 4.43/30 = -2.38
This means that an increase in the price of eggs by 1 unit will decrease the sales by 2.38 units.
Cross Price Elasticity
To calculate Cross Price Elasticity of Demand we are essentially looking for how the price of cookies impacts the sales of eggs. So we use the formula:
CPEcookies = (ΔQ/ΔPcookies) * (Pcookies/Q)
We know from our regression that (ΔQ/ΔPcookies) is the coefficient of Price of Cookies (-8.71).
We use the mean price of cookies and mean sales for the rest of the formula giving (4.37/30)
CPEcookies = -8.71 * (4.37/30) = -1.27
This means that an increase in the price of cookies by 1 unit will decrease the sales of eggs by 1.27 units.
Interpretation
We now know that the price of eggs and price of cookies are complementary to one another in this scenario. Since you only sell too products, one explanation could be that people who come in for cookies and eggs would rather get them elsewhere if the price is too high.
Also, it means that if you had to choose between a price cut on cookies or eggs, go with cookies!
Next steps
You are now in an ideal situation where you can run an optimization function to set the right price for both cookies and eggs.
This is out of the scope of this post, but if you’re interested in doing that check out R’s optim() function ~ or leave a comment below 😛
Bonus
Can you figure out what to do with the Ads?
I’ve included some ideas in the complete code below:
################################### # Warm-up ... data and stuff # ################################### # Load data and output summary stats sales.data<-read.csv('supermarket.csv') #Look at column names and their classes sapply(sales.data,class) # Change Ad.Type to factor and print Summary Stats sales.data$Ad.Type<-as.factor(sales.data$Ad.Type) summary(sales.data) #################### # Create Models # #################### # Load required library library(memisc) # Create models m1<-lm(formula=Sales~Price.Eggs,data=sales.data) m2<-update(m1,.~.+Ad.Type) m3<-update(m2,.~.+Price.Cookies) mtable(m1,m2,m3) #################### # DIAGNOSTICS # #################### # Linearity Plots par(mfrow=c(1,2)) plot(m3) par(mfrow=c(1,1)) # Multi-collinearity library(car) vif(m3) # variance inflation factors sqrt(vif(m3)) > 2 # problem? # Diagnosis: Nonlinearity crPlots(m3) # Diagnosis: Non-independence of Errors # We want a D-W Statistic close to 2 durbinWatsonTest(m3) ######################### # Price Elasticity # ######################### # Calculate Price Elasticity PE<-as.numeric(m3$coefficients["Price.Eggs"] * mean(sales.data$Price.Eggs)/mean(sales.data$Sales)) CPEcookies<-as.numeric(m3$coefficients["Price.Cookies"] * mean(sales.data$Price.Cookies)/mean(sales.data$Sales)) # Print Results PE CPEcookies #################################### # BONUS - What about the ads? # #################################### # Subset the data sales.adEggs <- subset(sales.data,Ad.Type==0) sales.adCookies <- subset(sales.data,Ad.Type==1) # Diagnostic on subsets' means and if they are different ... they are. wilcox.test(x=sales.adCookies$Sales,y=sales.adEggs$Sales,exact=F,paired=T) # On average, does the advert for eggs generate higher sales for eggs? mean(sales.adEggs$Sales) >= mean(sales.adCookies$Sales) |


Wow! Great example / tutorial and written with creativity and personal commentary. GOOD/BAD snippets.
Keep on posting! And maybe I can help you out in the future on preparing datasets.
Vincent “R” van Witteloostuyn
Hi Vincent,
Yes I would appreciate that! Thanks!!
Salem
Hey Salem, thanks for sharing this really helpful resource. I’m pretty new to R and am working with some data on public transit ridership, transit fare prices, and fuel prices. I was wondering if you could explain the “mtable” function you use in your example above—I was trying to replicate (for my own data) your table showing the “additive” effect of each new variable on the model, but I’m not sure how to get the table as an output…
Many thanks!
Hi Bora,
Sounds interesting, would love to see your study and findings.
The mtable function comes with the library “memisc” (see: http://cran.r-project.org/web/packages/memisc/memisc.pdf)
Salem
Pingback: Price Elasticity – Relationship between Price and Demand |
Hi Salem ,
A great blog on the use of R for price elasticity . Can you also describe the Optim() function in your blog or direct us to other links where we can read about the function
Regards
Soumitra
Very nice, thanks Salem,
I’d be very interested in the optimization part, that’s what i been looking for….
Can you show how you optimize after your linear regression ?
regards,
Mayouf
Hi Salem,
I have some doubts around price elasticity being a linear regression problem. I have seen people using linear regression with log transformed variables or even Quantile regression. So wanted to point out this
Regards,
Azim
Hey Salem, thanks for sharing this really helpful. Is it possible for you to publish or explain me how to create optimization function to set the right price for both cookies and eggs in R? I tried searching optim() function but unfortunately not able to implement here.
Good article.
I want to know what’s the best dataset to get from my database to process a price elasticity model.
I have the quantity and price per store (which are in states and has different types) and per day for the past 5 years and products (with 4 levels of hierarchy on top of the products).
I also have the discount applied to the price.
So… I extract the quantity sold and price for each day, state, store type, level 4 of the products.
Do I have to get the price with or without the discount?
Does going too far in the past has a positive or negative impact?
is it better to have a “constant price” amount instead of the real product price? (constant price = price of the product with the inflation included, 10$ there is 5 years ago is not 100$ today…)
Is it better to create 1 model for all the product group at the same time? or better to generate 1 model per group of product?
there is so many options possible, I’m not sure what’s better level of details we have to provide to process the model.
Thanks.
Hey,
Very wonderful post. Please let us know how to use optim function with the same.
hi there,
a really good and well understandable example. well prepared, and thank you!
Just one question – when you say “This means that an increase in the price of eggs by 1 unit will decrease the sales by 2.38 units.” – shouldn’t this be “percent” instead of “units”? If I understand correctly, then the coefficient itself (-16.12) indicates the unit-wise change and the elasticity should be the percent-wise change (?)
Thanks a lot!
You are right, check: https://rpubs.com/cyobero/elasticity for the correct interpretation. The equations used are equal.
Thank you Salem for sharing such an informative article!
Hey! Nice post. Could you please explain on how to find the optimal price of eggs to increase the revenue ie. sales divided by price?
This is a great article, really helpful. But think we can not use a simple OLS estimation because of endogeneity of your variables. Then what should be the approach?
Dear Salem, This is very helpful!
Can you please let me know how I can manage my decimal places of R2 in output?
Dear Salem,
What a wonderful post! It helps a lot! Thanks.
Regarding the optimum price, according Ian Khaw (https://www.linkedin.com/pulse/value-based-pricing-price-elasticity-optimum-ian-khaw), it could be easy calculated with the information of the cost price of the product:
Optimum Price = Price Elasticity x Cost / (Price Elasticity + 1)
The problem with this formula, is that if -1 < PE < 0 , it will result in a negative Optium Price. Is that the case of taking the absolute value?
I am right to assume that an elasticity between -1 and 0 means a inelastic demand (i.e. the delta variation in price will be greater than the delta variation in demand) thus it is not wise to change the price?
Hey Salem!!!,
Thanks for the post. It is really helpful to apply at work.
Looking forward for more posts like this and something on price optimization and cost optimization using R.
if there is seasonality dimension . How will the model look like ?